谐波分析原理以及在电路中的应用
谐波分析原理以及在电路中的应用:
谐波分析原理是什么:
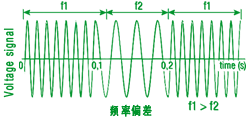
谐波分析原理是一种用于研究信号频谱特性的分析方法。它采用了傅里叶变换的思想,将任何非周期信号分解为一系列正弦波的叠加,从而得到信号的频谱分布情况。通过谐波分析,我们可以深入了解信号的频域特性,为信号处理、通信系统设计等领域提供重要的参考依据。
谐波分析的基本原理是将原始信号展开为谐波信号的叠加。任何复杂的周期信号都可以表示为若干个谐波信号的叠加,这些谐波信号的频率分别为原信号频率的整数倍。这是基于傅里叶级数理论得出的结论。根据这个原理,我们可以通过对信号进行傅里叶变换,将信号从时域转换到频域,得到信号的频谱分布。
在进行谐波分析时,一般会使用离散傅里叶变换(Discrete Fourier Transform,DFT)或者快速傅里叶变换(Fast Fourier Transform,FFT)等算法。这些算法可以高效地计算出信号的频谱信息,对于大规模数据的分析也具有一定的优势。
谐波分析在许多领域有着广泛的应用。在通信系统中,我们常常需要对信号进行频谱分析,以评估信道的带宽资源和抗干扰能力,以及对信号进行解调和调制等操作。在信号处理领域,谐波分析可以帮助我们了解信号的频率成分,从而采取相应的处理措施,例如滤波、降噪等。另外,在音频和视频处理领域,谐波分析也被广泛应用于音频合成、音乐分析、图像处理、视频编码等方面。
谐波分析不仅可以帮助我们理解信号的特性,还可以对一些问题进行故障诊断和故障排查。通过分析信号在频谱上的分布情况,我们可以判断出信号存在的谐波分量以及干扰因素,从而更好地优化系统性能。例如,在电力系统中,如果有谐波现象存在,可能会导致电力设备的不稳定和工作项目的故障,因此需要进行谐波分析并采取相应的补救措施。
谐波分析原理是一种研究信号频谱特性的重要方法。它通过分解信号为一系列谐波分量的叠加,帮助我们了解信号在频域上的分布情况,为信号处理、通信系统设计等领域提供技术支持。谐波分析的应用范围广泛,可以在通信、音视频处理、故障诊断等多个领域发挥重要作用。对于工程技术人员和研究人员来说,深入了解谐波分析原理及其应用是非常有益的。
谐波分析法在电路中的应用:
谐波分析法是一种重要的电路分析方法,它广泛应用于各种电路中。本文将探讨谐波分析法在不同类型电路中的适用性,并介绍其原理和实际应用。
谐波分析法是一种基于频域分析的方法,它通过将电路中的信号分解成不同频率的谐波分量来研究电路的性能。它可以帮助我们深入理解电路中的谐波失真、频率选择性、相位变化等问题,并提供有效的解决方案。
在不同类型的电路中,谐波分析法具有不同的适用性。首先,对于线性电路,谐波分析法非常适用。线性电路的特点是输入和输出之间存在线性关系,即输出信号是输入信号的简单倍数。在这种情况下,谐波分析法可以准确地描述输入信号和输出信号之间的谐波关系,并帮助我们分析电路的线性程度。
对于非线性电路,谐波分析法同样适用。非线性电路的特点是输入和输出之间存在非线性关系,即输出信号不是输入信号的简单倍数。在这种情况下,谐波分析法可以帮助我们找到非线性电路中各个谐波分量的幅度和相位,并进一步分析电路的非线性程度。
谐波分析法还适用于频率选择电路。频率选择电路是指可以选择特定频率的信号通过,而抑制其他频率的信号。谐波分析法可以帮助我们确定频率选择电路的通带和阻带范围,并分析电路的频率选择性能。
谐波分析法适用于各种类型的电路。它可以帮助我们了解电路中不同频率的谐波分量对电路性能的影响,进一步优化电路设计和分析。谐波分析法的原理比较简单,只需要对输入信号进行频域分析即可获得电路的谐波响应。然而,在实际应用中,谐波分析法需要借助一些专业的工具和软件,如示波器、谐波分析仪等。
除了在电路分析中的应用,谐波分析法还在其他领域有着广泛的应用。比如,在电力系统中,谐波分析法可以帮助我们分析电力质量问题,如谐波污染、谐波失真等,并提供相应的解决方案。在音频系统中,谐波分析法可以帮助我们分析音频信号的谐波成分,进一步改善音频质量。
谐波分析法是一种重要的电路分析方法,适用于不同类型的电路。通过谐波分析法,我们可以深入了解电路中不同频率的谐波分量对电路性能的影响,并提供相应的解决方案。在实际应用中,我们需要借助专业的工具和软件来实现谐波分析,以获得准确的结果。谐波分析法的应用还不仅限于电路,还可以在电力系统、音频系统等领域起到重要作用。通过深入研究和应用谐波分析法,我们可以进一步提高电路设计和优化的水平,为各个领域的发展做出贡献。
文章版权备注
- 2024-09-11电能质量控制装置是什么样的
- 2024-09-11电能质量监测终端检测技术规范
- 2024-09-10电能质量监测系统的作用和意义
- 2024-09-10电力分析仪的使用方法和作用有哪些
- 2024-09-10电力分析仪的作用和应用
- 2024-09-10电能质量与电力监测系统下的数据安全













 沪公网安备31011702889685
沪公网安备31011702889685
